پیشگفتار : جامعه های مختلف در آزمون های پارامتری و غیر پارامتری فقط با لحاظ صفت متغیر مورد بررسی و مقایسه قرار می گیرد.
اینک این سوال مطرح است که آیا واقعا فقط با یک صفت متغیر می توان جامعه های مورد بررسی را با هم مقایسه کرد.
طبیعی است جواب سوال مثبت نیست، در آزمون های Z، T وf افراد جامعه را فقط نسبت به صفت متغیر (x) مورد مطالعه قرار داده ایم در مورد همبستگی و رگرسیون دو یا چند متغیره نیز، مطالعه یک جامعه درباره دو یا چند متغیر یا صفت صورت می گیرد.
در واقع، این نوع تحلیل یک نوع تحلیل چند متغیره است.
حال در اینجا k متغیر را در نظر گرفته و آن را تحلیل کرده و سعی می کنیم که تعریف تحلیل چند متغیره تا حدودی تکمیل گردد.
برای این کار از هر فرد نمونه (فرد جامعه)، k صفت x1,x2,x3,…xk را اندازه می گیریم.
می خواهیم که آیا جامعه مورد نمونه گیری ما از حیث کلیه متغیرها مورد مطالعه وضع مشخصی دارد تا به طور روشن و اشکار قابل تشخیص باشد، یا در قیاس 2 یا چند جامعه این سوال مطرح می شود که آیا از حیث کلیه k، صفت متغیر مورد بررسی با هم یکی هستند یا خیر.
بر این اساس می توان صفات مشخصه جامعه را از هم جدا کرد.
مقدمه :
تحلیل واریانس به روشی گفته می شود که در آن، تغییر مشاهده شده در داده های آزمایشی به بخش های مختلفی تقسیم می شود و هر کدام از بخشهای به دست آمده دارای منبع مشخص و شناخته شده ای است.
مقدار نسبی تغییر حاصل مورد بررسی قرار می گیرد و تعیین می شود که آیا بخش معینی از تغییر با توجه به فرضیه صفر تدوین شده، بزرگتر از انتظار است یا خیر؟
تحلیل واریانس، به طور تنگاتنگی با طرح آزمایش ها در ارتباط است.
بدیهی است که هرگاه بخشهای مختلف تغییر به اثرهای معینی ارتباط داده شوند، آزمایشها را باید چنان طرح کرد که امکان چنین امری را به شیوه ای منطقی و دقیق فراهم سازند(فرگوسن و تاکانه، ترجمه دلاور و نقشبندی، 1387).
در آمار تجزیه واریانس به بخش های مختلف امری متداول است.
شیوه ای که به این منظور به کار برده می شود، تحلیل واریانس نامیده می شود.
این روش به وسیله ر.ا.فیشر گسترش یافت که گزارش آن در سال 1923 منتشر شد.
کاربرد اولیه این روش محدود به حوزه کشاورزی بود، ولی از آن زمان تا به حال در بسیاری از زمینه های آزمایشی کاربرد گسترده ای یافته است (فرگوسن و تاکانه، ترجمه دلاور و نقشبندی، 1387).
در پژوهش حاضر سعی بر آن است که یکی از انواع تحلیل واریانس به نام تحلیل واریانس چند متغیری (MANOVA) مورد تجزیه و تحلیل قرار گیرد.
تحلیل واریانس چند متغیره(MANOVA) :
تحلیل واریانس چند متغیره (MANOVA) نوعی بسط تحلیل واریانس است که از آن هنگامی استفاده می شود که بیش از یک متغیر وابسته داشته باشیم.
این متغیرهای وابسته باید به نوعی ارتباط داشته باشند، یا باید یک دلیل مفهومی برای کنار هم قرار گرفتن آنها وجود داشته باشد.
MANOVA گروهها را مقایسه می کند و به شما می گوید که آیا میانگین تفاوت بین گروهها در ترکیبی از متغیرهای وابسته ناشی از شانس بوده است.
برای این کار MANOVA یک متغیر وابسته خلاصه جدید ایجاد می کند که ترکیب خطی از هریک متغیرهای وابسته اصلی است.
سپس تحلیل واریانس را با استفاده از این متغیر وابسته مرکب انجام می دهد.
MANOVA به شما می گوید که آیا تفاوت معناداری بین گروهها از لحاظ این متغیر وابسته مرکب وجود دارد یا خیر؛ همچنین نتایج تک متغیره را برای هر یک از متغیرهای وابسته به طور جداگانه ارائه می دهد (پلنت؛ ترجمه کاکاوند، 1389).
ساختار Manova شبیه به ساختار Anova است با این تفاوت که طرح های Manova دارای عبارت هایی برای متغیرهای وابسته چندگانه است.
در این طرح با این مسئله سر و کار داریم که آیا متغیرهای مستقل ارائه شده اثری بر متغیرهای وابسته دارد یا نه.
مثلاً آزمایشی که در آن بیش از یک متغیر وابسته وجود دارد را اجرا کرده ایم.
اگر بخواهیم از طرح Anova استفاده کنیم لازم است برای هر متغیر وابسته یک تحلیل تک متغیره اجرا کنیم که این روش خود دو عیب دارد:
اول این که تورم فوق العاده خطای نوع اول و دوم در آن دیده می شود ، دوم این که عدم توانایی پژوهشگر در به حساب آوردن همبستگی میان متغیرهای وابسته در آن مشهود است و این عواقب منجر به نادرستی استخراج و تفسیر نتایج می شود.
علاوه بر این باید در نظر داشت که تحلیل تک متغیری نمی تواند همبستگی های درونی بین متغیرهای وابسته را اندازه گیری کند.
در Manova هر دو مسئله همزمان با یکدیگر کنترل می شود و همچنین همبستگی بین متغیرهای وابسته را به حساب می آورد.( Manova با تحلیل خطی بهینه (چند متغیری) متغیرها سر و کار دارد ) .
همچنین در Manova، مجموع مجذورات با مقادیر ماتریس سر و کار دارد.
البته در این مدل ماتریس، مجموع مجذورات و حاصلضرب آنهاست.
با توجه به اینکه یک ترکیب خطی ممکن است برای توجیه همه واریانس در N متغیر وابسته کافی نباشد، بنابراین Manova ترکیب خطی دوم را طوری استخراج می کند که مستقل از نخستین ترکیب باشد و واریانس باقیمانده را بیشینه سازد.
سپس ترکیب سوم به گونه ای که متعامد با نخستین و دومین ترکیب است و واریانس باقیمانده را بیشینه سازد استخراج می کند و این عمل تا حصول یک ملاک معین ادامه دارد.
بطور کلی ویژگی های مهم آزمون تحلیل واریانس چند متغیری شامل موارد زیر است:
1. ارزش ویژه، شاخص تمرکز واریانس مشترک بین اثر Manova و یک ترکیب خطی از متغیرهای وابسته چندگانه است.
2. همه مشخصه های آزمون Manova به عنوان تابعی از ارزش های ویژه محاسبه می شود.
3. ضرایب تابع تشخیص به عنوان تابعی از ارزش های ویژه محاسبه می شود.
4. ارزش های ویژه اطلاعاتی درباره اهمیت نسبی متغیرهای وابسته در ترکیب های خطی بهینه به دست می دهند. در روش MANOVA ماتریس حاصلضرب برداری کل (T) به دو گروه ماتریس حاصلضرب برداری بین گروه ها (B) و ماتریس حاصلضرب برداری درون گروه ها(W) تفکیک می شود.
T=B+W Tمیزان انحراف نمونه ها از میانگین را در هر سطح متغیر مستقل یا گروه از میانگین کل هر متغیر وابسته را نشان می دهد.
ماتریس B اثرات متفاوت تدابیرآزمایشی را روی مجموعه متغیرهای وابسته نشان می دهد.
در نهایت W نشان می دهد که نمونه ها در هر سطح یا گروه متغیر مستقل چگونه از میانگین های متغیرهای وابسته منحرف می شوند.
چهار آزمون آماری متعارف در این زمینه وجود دارد:
اثر پیلایی، لامبدای ویلکز، اثر هتلینگ و روش بزرگترین ریشه دوم. پرکاربردترین این آماره ها لامبدای ویلکز می باشد که براساس نسبت Wبر B+Wساخته می شود.
در عمل اگر اثرمتغیر مستقل بر متغیرهای وابسته از نظر آماری معنادار باشد، یعنی اگر تدابیرآزمایشی اثرگذار باشند، در اینصورت مقدار B نسبتا بزرگ و Wکوچک خواهد بود(لارنس و همکاران؛ ترجمه پاشا شریفی و همکاران، 1391).
بنیانگذاران آزمون :
اصول کلی تحلیل واریانس ابتدا توسط سر رونالد فیشر در سال 1919 ابداع شد.
و سپس جزییات آن توسط سایر آمار دانان تکمیل شد.
نوع آزمون (شرح علت پارامتریک ؛ ناپارمتریک و ...) :
آزمون تحلیل واریانس چند متغیری جزء آزمون های پارامتریک محسوب می شود دلایل آن به شرح زیر می باشد:
1. هر یک از موارد مشاهده شده مستقل است، یعنی اینکه انتخاب یک مورد به انتخاب مورد دیگری وابسته نیست.
2. واریانس نمونه ها برابر یا تقریبا برابر است.
3. توصیف متغیرها براساس مقیاس فاصله ای یا نسبی انجام می گیرد.
4. توزیع نمره ها در جامعه نرمال (بهنجار) یا نزدیک به توزیع بهنجار است(پاشا شریفی و نجفی زند، 1380).
شرایط استفاده از آزمون (در مقیاس اسمی ، داده های ترتیبی و ..) :
مفروضه های به کار گیری این آزمون عبارتند از:
سطح اندازه گیری. یکی از مفروضه های این آزمون این است که متغیر وابسته در سطح نسبی یا فاصله ای اندازه گیری شده باشد؛ یعنی استفاده از مقیاس پیوسته به جای طبقه های مجزا.
نمونه گیری تصادفی. باید نمره ها با استفاده از نمونه تصادفی از جامعه به دست آمده باشند.
استقلال مشاهدات. مشاهداتی که داده ها را تشکیل می دهند باید مستقل از یکدیگر باشند؛ یعنی هر مشاهده با اندازه گیری نباید تحت تاثیر مشاهده یا اندازه گیری دیگر باشد.
توزیع بهنجار. در روش های پارامتریک، فرض بر این است که جامعه ای که نمونه از آن گرفته می شود توزیع بهنجار داشته باشد.
همگنی واریانس. یکی دیگر از مفروضه های تحلیل واریانس چند متغیره این می باشد که نمونه ها از جامعه هایی با واریانس برابر به دست آمده باشند. این بدین معنی است که تغییر پذیری نمره های هر گروه مشابه است.
برای آزمون این مسئله، SPSS آزمون لوین را برای برابری واریانس ها به عنوان بخشی از تحلیل های تحلیل واریانس اجرا می کند(پلنت؛ ترجمه کاکاوند، 1389).
این چند مفروضه بالا برای تمام آزمون های پارمتریک می باشد.
در ادامه چند مفروضه اختصاصی برای آزمون تحلیل واریانس چند متغیره را ذکر می کنیم:
1- اندازه نمونه باید مورد هایی بیشتر از تعداد متغیرهای وابسته در هر خانه داشته باشیم.
در بهترین حالت، باید بیشتر از این مقدار داشته باشید، ولی این حداقل مطلق است. داشتن نمونه بزرگتر به ما کمک می کند تخطی از برخی مفروضه های دیگر (مثل بهنجاری) نتایج پژوهش را منحرف نکند.
2- بهنجاری اگر چه آزمون های معنادارری MANOVA مبتنی بر توزیع بهنجار چند متغیره هستند ولی در عمل این روش در مقابل تخطی های ناچیز ار حالت بهنجار مقاوم است. طبق گفته تاباکنیک فیدل (2007) اندازه نمونه حداقل 20 مورد در هر خانه می تواند این مقاومت را تضمین کند.
3- پرت ها MANOVA حساسیت خیلی زیادی به پرت ها دارد (یعنی داده ها یا نمره هایی که با بقیه نمره ها تفاوت دارد). باید پرت های تک متغیره (به طور جداگانه برای هر یک از متغیر های وابسته) و پرت های چند متغیره را بررسی کنید. پرت های چند متغیره افرادی هستند که ترکیب عجیبی از نمره ها را در متغیر وابسته دارند (مثلا نمره خیلی بالا در یک متغیر و نمره خیلی پایین در متغیر دیگر).
4- خطی بودن این مفروضه به وجود رابطه خطی مستقیم بین هر جفت از متغیرهای وابسته اشاره دارد. این مسئله را می توان به چند طریق ارزیابی کرد، که ساده ترین راه ایجاد ماتریس نمودار های پراکندگی بین هر جفت از متغیرها برای گروهها می باشد.
5- همگنی رگرسیون این مفروضه فقط در صورتی مهم است که بخواهید تحلیل رو به پایین انجام دهید. این روش هنگامی به کار می رود که علت نظری یا مفهومی برای رتبه بندی (مرتب کردن) متغیرهای وابسته خود داشته باشید.
6- هم خطی چند گانه و واحد بودن MANOVA هنگامی که متغیر های وابسته فقط در حد متوسطی همبستگی داشته باشند به بهترین شکل عمل می کند. در صورت وجود همبستگی های پایین، باید اجرای تحلیل واریانس تک متغیره جداگانه را برای متغیرهای وابسته مختلف خود در نظر بگیرید. وقتی متغیرهای وابسته همبستگی بسیار زیادی داشته باشند، به این مسئله هم خطی چند گانه می گویند. این حالت زمانی رخ می دهد که یکی از متغیرها ترکیبی از متغیر های دیگر است. به این حالت واحد بودن می گویند و با شناخت متغیرها و نحوه به دست آوردن نمره ها می توان از آن جلوگیری کرد.
7- همگنی ماتریس های واریانس-کوواریانس خوشبختانه آزمون این مفروضه به عنوان بخشی از خروجی MANOVA ایجاد می شود(پلنت؛ ترجمه کاکاوند، 1389).
کاربرد آزمون (همبستگی رابطه ها ؛اثر و نقش ، تفاوت یا مقایسه ها ) :
اغلب اتفاق می افتد زمانی که هدف محقق بررسی بیش از یک متغیر وابسته است، به جای استفاده از روش های چند متغیری هر بار یکی از متغیرهای وابسته را در نظر گرفته و از روش ANOVA برای تحلیل استفاده می نماید.
استفاده از این روش می تواند اشکالاتی را به وجود آورد که در ادامه به بیان آن ها می پردازیم :
1. آزمون های آماری تک متغیری به طور معمول همبستگی متقابل متغیرهای وابسته را نادیده می گیرد. در حالیکه روش MANOVAهمبستگی متقابل بین متغیرهای وابسته را با بررسی ماتریس های واریانس کواریانس در نظر می گیرد.
2. روش MANOVA محققان را قادر می سازد تا روابط بین متغیرهای وابسته را در هر سطحی از متغیرهای مستقل بررسی کنند.
3. این روش به شناسایی متغیرهای وابسته با بیشترین توان تفکیک در گروه بندی کمک می کند. MANOVAبه واسطه توان افزایش یافته در موقعیت چند متغیری می تواند تفاوت های گروهی نامشخص تحت شرایط تحلیل های آماری تک متغیری را آشکار نماید.
4. روش MANOVA سطح آلفای کلی یا میزان خطای نوع اول (یعنی احتمال این که فرض صفر درست بوده و به اشتباه رد شود)را کنترل می کند. برای مثال اگر بخواهیم تفاوت های جنسیتی(متغیر مستقل) را با چهار متغیر وابسته رضایت شغلی )پرداخت، مزایا، همکاران و محل کار) بررسی کنیم و برای این کار از چهار آزمون جداگانه t و یا روش ANOVAاستفاده نماییم، با سطح خطای 5% برای هر آزمون با خطای نوع اول برابر 0.054 مواجه خواهیم شد.
در این حالت استفاده از روش MANOVA این مشکل را برطرف می کند (لارنس و همکاران؛ ترجمه پاشا شریفی و همکاران، 1391).
حل مثال با نرم افزار spss :
دو گروه 80 نفری از بیماران مبتلا به دیابت و افراد سالم به عنوان نمونه مورد پژوهش در دست داریم.
از افراد دو گروه آزمون هوش هیجانی گرفته می شود و می خواهیم بدانیم که آیا بین دو گروه در مولفه های هوش هیجانی تفاوت وجود دارد یا نه؟
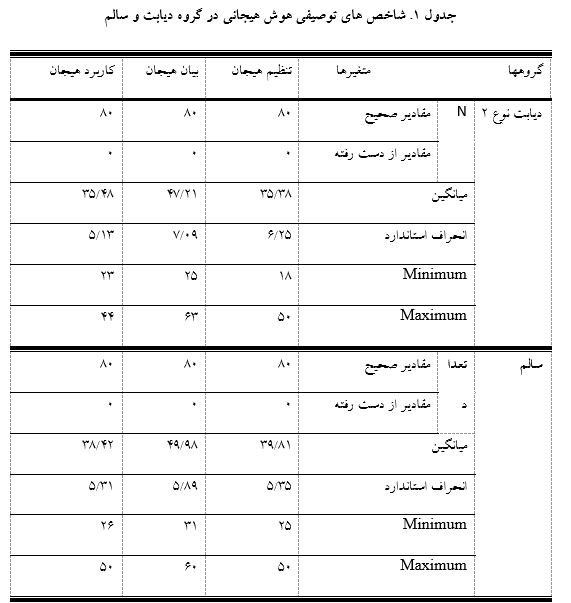
در جدول 1 شاخص های توصیفی دو گروه آورده شده است:
جدول 1 نشان می دهد میانگین و انحراف استاندارد در گروه دیابت نوع 2 در مولفه تنظیم هیجان برابر با38/35 و 25/6، بیان هیجان برابر با 21/47 و09/7 ، کاربرد هیجان برابر48/35 و 13/5 می باشد. میانگین و انحراف استاندارد در گروه سالم در مولفه تنظیم هیجان برابر با81/39 و35/5، بیان هیجان برابر با 98/49 و89/5، کاربرد هیجان برابربا 42/38 و31/5 12 می باشد.
قبل از بررسی تحلیل واریانس چند متغیره (MANOVA)، آنچه که باید درنظر گرفته شود، مباحث مربوط به رعایت کردن و بررسی کردن مفروضه های آماری است.
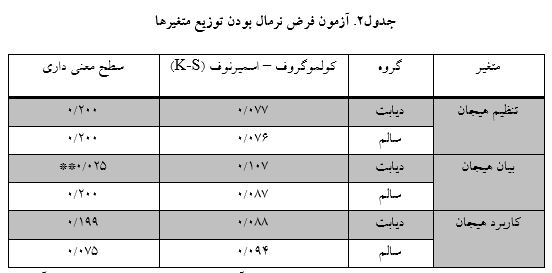
از جمله پیش فرض هایی که در تحلیل واریانس چند متغیره (MANOVA)منظور میگردد، فرض نرمال بودن توزیع با استفاده از آزمون (کولموگروف – اسمیرنوف ) یا (K-S) است. این بررسی روی متغیرهای پژوهش انجام شد.
همانطور که از یافته های جدول 2 استنباط می شود، از آنجا که سطح معنیداری به دست آمده در آزمون (K-S)، در اکثر متغیر های پژوهش به تفکیک گروه، بیش از مقدار ملاک 05/0 می باشد، در نتیجه می توان گفت که توزیع متغیر های مورد بررسی در نمونه آماری داری توزیع نرمال می باشد و می توانیم فرضیه های پژوهش را از طریق آزمون های پارامتریک مورد آزمون قرار دهیم.
جهت تجزیه و تحلیل داده های مربوط به تفاوت بین دو گروه بیماران دیابت نوع 2 و افراد سالم از لحاظ مولفه های هوش هیجانی، از روش تحلیل واریانس چند متغیره (مانوا) بهره گرفته شد.
قبل از به کار گیری این آزمون مفروضه های این آزمون به وسیله آزمون باکس، لامبدای ویلکز و آزمون لون مورد بررسی قرار گرفت.
به همین منظور برای بررسی پیش فرض همگنی ماتریس واریانس - کوواریانس مولفه های هوش هیجانی در گروه های مورد پژوهش نیز از آزمون باکس استفاده شد.
نتایج آزمون باکس در جدول 3 آمده است:
جدول 3 نشان می دهد مقدار سطح معناداری(05/ 0 p>) می باشد که گویای آن است شرط همگنی ماتریس واریانس –کواریانس به خوبی رعایت شده است (125/1 = F و 05/0P> ).
برای تعیین معنی داری اثر گروه بر مولفه های هوش هیجانی، از آزمون لامبدای ویلکز استفاده شد که نتایج حاصل در جدول 4 گزارش شده است:
نتایج آزمون لامبدای ویلکز نشان می دهد که بین دو گروه حداقل در یکی از مولفه های هوش هیجانی ( تنظیم هیجان، بیان هیجان و کاربرد هیجان) تفاوت معنادار وجود دارد(364/9= (3و156)F و 01/0P< ).
برای بررسی پیش فرض برابری واریانس های مولفه های هوش هیجانی در گروه های مورد پژوهش نیز از آزمون لون استفاده شد.
نتایج آزمون لون در جدول 5 آمده است:
جدول فوق گویای آن است که واریانس های مولفه های هوش هیجانی در دو گروه با هم برابر بوده و با یکدیگر تفاوت معنی داری ندارند، که این یافته، پایایی نتایج بعدی را نشان می دهد.
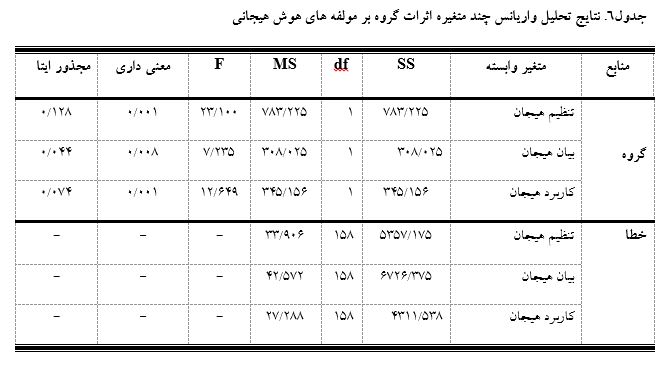
با توجه به نتایج به دست آمده از آزمون های باکس، لامبدای ویلکز و لون، تحلیل های مربوط به اثرات بین آزمودنی ها مورد بررسی قرار گرفت که نتایج به دست آمده در جدول شماره 6 قابل مشاهده است:
براساس جدول6، بین دو گروه بیماران مبتلا به دیابت نوع 2و افراد سالم، در مولفه تنظیم هیجان (100/23= (158و1)F و 01/0 P<) تفاوت معنادار وجود دارد. به این صورت که نمره تنظیم هیجان گروه دیابت به طور معناداری پایین تر از سالم است. متغیر گروه 8/12درصد واریانس تنظیم هیجان را تبیین می کند.
بین دو گروه بیماران مبتلا به دیابت نوع 2و افراد سالم، در بیان هیجان (235/7= (158و1)F و 01/0P< ) تفاوت معنادار وجود دارد. به این صورت که نمره بیان هیجان گروه دیابت به طور معناداری پایین تر از گروه سالم است. متغیر گروه 4/4 درصد واریانس بیان هیجان را تبیین می کند.
بین دو گروه بیماران مبتلا به دیابت نوع 2و افراد سالم، در کاربرد هیجان (649/12= (158و1)F و 01/0P< )، تفاوت معنادار وجود دارد.
به این صورت که نمره کاربرد هیجان گروه دیابت به طور معناداری پایین تر از گروه سالم است.
متغیر گروه 4/7 درصد واریانس کاربرد هیجان را تبیین می کند.
دانلود این مقاله به همراه منابع و پیوست ها