برای بررسی ارتباط میان متغیرهای اسمی چهار نوع ضریب همبستگی تحت عناوین ضریب همبستگی پیوستگی (Contingencycoefficicent) ضریب فی و V کرامر (Phi and Cramer's V)، لمبدا (Lambda) و ضریب غیر قطعی (Uncertainy coefficient) در نرم افزار SPSS وجود دارد که در ادامه به اختصار توضیح داده می شوند.
ضریب همبستگی
ضریب همبستگی شاخصی از ارتباط میان دو متغیر اسمی است که دست کم یکی از آن ها دارای بیش از دو مقوله باشد و براساس آماره ی مجذور کای آزموده می شود.
ارزش عددی این ضریب همبستگی بین صفر تا 1 متغیر است و حداکثر ارزش ضریب همبستگی به تعداد مقوله های (سطوح متغیرهای اسمی) ردیفی و ستونی در یک جدول متقاطع وابسته است.
به طور مثال، از این ضریب می توان برای بررسی ارتباط میان جنسیت و علاقه به رشته تحصیلی (ریاضی، تجربی و انسانی) استفاده کرد.
توجه داشته باشید که کاربرد این آزمون مستلزم وجود یک ارتباط منطقی میان متغیرهای اسمی است.
به طور مثال، فرض می شود که علاقه به رشته ها از جنسیت آزمودنی ها اثر می پذیرد. شاید نیاز به ذکر نباشد که بررسی ارتباط میان جنسیت و قومیت به دلیل ماهیت غیرمرتبط آن ها، منطقاً قابل مطالعه نیست.
ضریب همبستگی فی کرامر:
برای بررسی ارتباط میان دو متغیر اسمی که هر کدام دارای دو سطح هستند ضریب همبستگی فی کرامر مناسب است.
به طور مثال، ضریب همبستگی فی را می توان جهت بررسی ارتباط میان جنسیت و سیگاری بودن به کار برد.
اگر فرمول ضریب همبستگی پیرسون را بر روی متغیرهای دو مقوله ای به کار ببریم، به ضریبی که از این روش به دست می آید، ضریب همبستگی فی گفته شود.
ضریب همبستگی لاندا:
این شاخص یک ضریبی از ارتباط میان دو متغیر اسمی است که به کاهش نسبی خطا در پیش بینی متغیر وابسته برحسب متغیر مستقل اشاره دارد.
ضریب لاندای 1 نشان دهنده ی آن است که متغیر مستقل به طور کامل متغیر وابسته را پیش بینی می کند و ضریب لاندای صفر نشان دهنده آن است که متغیر مستقل هیچ کمکی به پیش بینی متغیر وابسته نمی کند.
توجه داشته باشید در هنگامی که دو متغیر از لحاظ ارتباط آماری مستقل هستند، ضریب لاندا برابر با صفر می شود، اما صفر بودن ضریب لاندا لزوماً به معنی مستقل بودن دو متغیر از یکدیگر نیست.
بنابراین، هنگامی که پژوهشگر با همبستگی صفر مواجه می شود، بهتر است با روش های دیگر ارتباط میان متغیرها را وارسی کند.
ضریب لاندا به دو صورت نامتقارن و متقارن محاسبه می شود.
اگر محاسبه ی دو لاندا (لاندای 1 و لاندای 2) بسته به این که کدام متغیر را مستقل و کدام را وابسته در نظر بگیریم متفاوت باشند، به آن لاندای نامتقارن می گویند، اما در حالت متقارن، بسته به این که کدام متغیر را مستقل و کدام را وابسته قرار دهیم، تفاوتی نمی کند.
نحوه ی محاسبه ی لاندای 1 و 2 در یک مثال پژوهشی توضیح داده می شود.
مثال پژوهشی:
بررسی ارتباط میان جنسیت و علاقه به رشته های تجربی، ریاضی و انسانی.
فرضیه پژوهشگر:
میان جنسیت و علاقه به رشته رابطه وجود دارد.
فرض کنید پژوهشگری عقیده دارد که پسران به رشته ی ریاضی و دختران به رشته های تجربی و انسانی گرایش دارند.
اگر این فرضیه کاملاً صحیح باشد، برحسب علاقه به رشته ی ریاضی، پسر بودن آزمودنی ها و برحسب علاقه به رشته تجربی و انسانی دختر بودن آزمودنی ها را به طور کامل و بدون خطا می توان پیش بینی کرد.
اما اگر بخواهیم از طریق جنسیت علاقه به رشته را پیش بینی کنیم، میزانی از خطا بروز پیدا می کند.
به طور مثال، اگر فرضیه ی پژوهشگر کاملاً صحیح باشد، می توان برحسب پسر بودن و بدون خطا، علاقه به ریاضی را مشخص کرد.
اما با توجه به دختر بودن، نمی توان گفت کدام یک از دختران به رشته ی تجربی و کدام به رشته ی انسانی علاقه مند هستند.
بنابراین، اگر متغیر جنسیت را وابسته و متغیر علاقه به رشته را مستقل فرض کنیم، ضریب لاندای اول برابر با یک و اگر معکوس عمل کنیم، یعنی جنسیت را متغیر مستقل و علاقه به رشته را متغیر وابسته فرض کنیم، لاندای دوم کمتر از 1 خواهد شد.
ضریب عدم قطعیت:
ضریب عدم قطعیت میزان کاهش خطا در پیش بینی یک متغیر را بر حسب یک متغیر دیگر نشان می دهد.
همانند آزمون لاندا، این ضریب برای بررسی روابط میان متغیرهای اسمی مناسب است.
به طور مثال، مقدار ضریب 76/0 نشان دهندهی آن است که بر حسب متغیر x، خطای ناشی از پیش بینی متغیر y در حد 76 درصد کاهش پیدا می کند.
ضریب کاپای کوهن:
ضریب کاپای کوهن شاخصی از ارتباط است که میزان توافق میان دو ارزیاب را پیرامون یک مجموعه از اشیاء یا افراد ارزیابی می کند.
این ضریب توافق (کاپا) به این دلیل که نسبت ارزیابی های ناموفق را ارزیابی های موافق اصلاح و کم می کند، همیشه کمتر از ضریب توافق کندال می باشد.
مهم ترین کاربرد ضریب کاپا در موقعیت هایی است که بخواهیم امکان عضویت گروهی افراد را پیش بینی کنیم.
به طور مثال، فرض کنید پژوهشگری عقیده دارد که بر حسب یک سری از نشانه های جسمانی یا روانی، می تواند امکان ابتلا به یک بیماری، حادثه و ... را پیش بینی کرد.
در چنین شرایطی، پژوهشگر افراد را بر اساس نشانه های مورد نظر به دو یا چند گروه (حادثه دیده و حادثه ندیده، سیگاری شدن و عدم سیگاری شدن و ...) تقسیم می کند و در طی یک روند زمانی، شرایط آزمودنی ها را ارزیابی می کند.
اگر پیش بینی پژوهشگر صحیح باشد، باید افرادی که توسط پژوهشگر به عنوان گروه خطر بالا شناسایی شده اند، بعد از یک دوره ی زمانی معین به آن حادثه یا آن رویداد خاص دچار شوند و کسانی که به عنوان گروه سالم شناسایی شده اند، بعد از گذشت مدت معین به آن رویداد ویژه دچار نشوند.
ضریب کاپا ارتباط میان دو حالت (ارزیابی اولیه ی پژوهشگر و عضویت گروهی آزمودنی ها در آینده) را بررسی می کند.
آزمون ریسک:
این آماره ارتباط میان حضور یک عامل و وقوع یک رویداد را بررسی می کند به طور مثال، خوردن صبحانه و جا نیانداختن واژگان در املاء دانش آموزان دبستانی.
در این آزمون اگر فاصله اطمینان برای شاخص آماری مربوط ارزش یک را دربربگیرد، نشان دهنده ی آن است که میان وقوع یک رویداد و حضور یک عامل رابطه ای وجود ندارد.
مثلاً برای بررسی رابطه ی میان مشاهده ی ابر در آسمان و وقوع بارندگی می توان از آماره ی ریسک استفاده کرد.
آماره ی کاکران و مانتل- هنزل (Cochran's and Mantel- Hanszel Statistics) آماره ی کاکران و مانتل- هنزل می تواند برای آزمودن استقلال میان یک عامل دو سطحی و یک پاسخ دو سطحی با توجه به کنترل یک متغیر مقوله ای دیگر به کار گرفته شود.
فرض کنید قرار است ارتباط میان شرکت و عدم شرکت در یک دوره ی آموزشی ویژه، با موفقیت و شکست در یک آزمون زبان انگلیسی بررسی شود و در عین حال، نقش جنسیت نیز کنترل شود.
ممکن است پژوهشگر عقیده داشته باشد که بین متغیر مشارکت در دوره ی ویژه و موفقیت در درس زبان انگلیسی رابطه وجود دارد و این ارتباط در سطوح گوناگون یک متغیر دیگر (مثلاً جنسیت) متفاوت و یا یکسان است.
بنابراین، آماره ی کاکران و مانتل0 هنزل دو پاسخ به شرح زیر فراهم می کند؛
1- بررسی ارتباط میان دو متغیر مورد نظر و
2- مقایسه ی نسبت های میان دو متغیر در سطوح متغیر سوم در صورتی که نسبت موفقیت و شکست برای دختران و پسران یکسان و یا نسبتاً یکسان باشد، آماره ی Torane Broslow-Day در خروجی های آماره ی کاکران و مانتل- هنزل از لحاظ آماری غیر معنی دار می شوند.
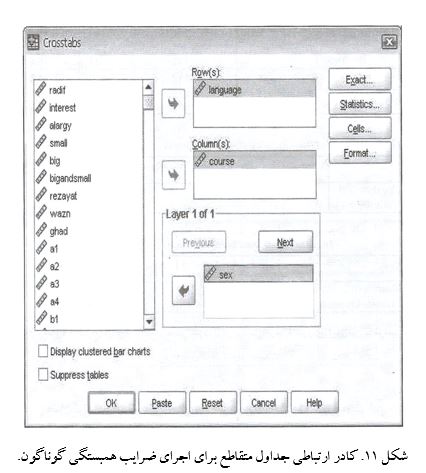
تمام ضرایب همبستگی و شاخص های آماری مربوط به ارتباط میان متغیرها (به جز ضریب اسپیرمن) که تاکنون توضیح داده شدند، در نرم افزار SPSS به شرح زیر قابل دسترسی هستند.
- از سربرگ Analyze، گزینه ی Descriptive Statistics و از انشعابات آن گزینه ی Crosstabs را انتخاب کنید.
- به دلخواه یکی از متغیرها را در جعبه ی Row و دیگری را در جعبه ی Columm قرار دهید.
- برای اجرای آزمون کاکران مانتل- هنزل علاوه بر مرحله ی مذکور، متغیر کنترل را که در مثال مربوط جنسیت فرض شده است، در جعبه ی زیرین Layer 1 of 1 قرار دهید.
- برای انتخاب ضریب همبستگی مناسب بر دکمه Statistics کلیک کنید و گزینه ی همبستگی مورد نظر را علامت دار نمایید.
از کادرهای ارتباطی خارج شوید و سپس بر گزینه ی ok کلیک کنید تا فرمان اجرا شود.
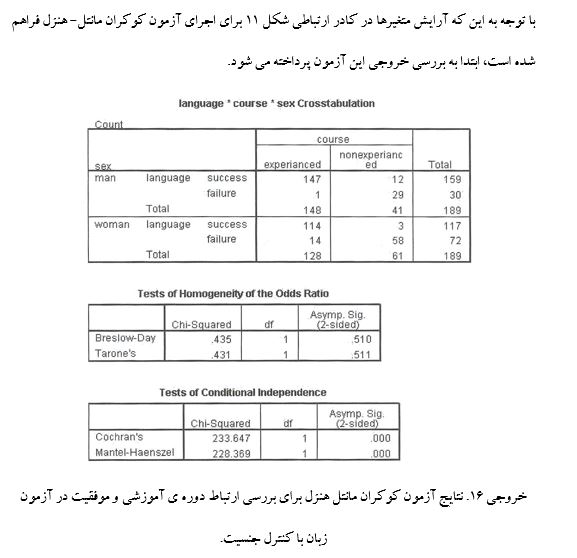
همان گونه که در نخستین جدول از خروجی 16 مشاهده می شود، در این مثال فرضی 147 نفر از مردان آموزش دیده در آزمون زبان موفق و تنها یک نفر از آن ها ناموفق بوده است.
همچنین، در زنان نیز وضعیت مشابه مردان است.
از 128 نفر زن آموزش دیده 114 نفر در آزمون زبان موفق و 14 نفر ناموفق بوده اند.
مقدار مجذور کای آزمون Breslow-Day (435/0) با سطح معنی 510/0< P و آزمون Tarone's (431/0) با سطح معنی داری 511/0< P نشان دهنده ی آن هستند که نسبت شانس موفقیت برای مردان و زنان شرکت کننده در دوره آموزشی تفاوت معنی داری نمی کند؛ به عبارت دیگر، اثر دوره ی آموزشی متأثر از جنسیت نیست.
خروجی آماره ی کوکران و مانتل- هنزل در سومین جدول به ترتیب مقادیر مجذور کای 647/233 و 369/228 و با سطح معنی داری 0001/0 > P، اثر دوره ی آموزشی را بر موفقیت در آزمون زبان پس از کنترل متغیر جنسیت، معنی دار نشان می دهد.
در خروجی 17، ارتباط میان علاقه به رشته تجربی، ریاضی و انسانی با جنسیت آزمودنی ها به روش ضریب لاندا و ضریب عدم قطعیت بررسی می شود.
همان گونه که در خروجی 17 مشاهده می شود، سه ارزش متفاوت در ستون Value از ضریب لاندا برای ارتباط میان Sex و interest (علاقه به رشته) ارائه شده است.
هنگامی که علاقه به رشته فرض شود، بر حسب جنسیت Sex می توان به مقدار 268/0 به پیش بینی علاقه به رشته کمک کرد.
اماهنگامی که جنسیت وابسته فرض شود، بر حسب علاقه به رشته می توان به مقدار 595/0 به پیش بینی جنسیت افراد دست یافت.
در سطر متقارن Symmetric به تقریب معدل، ضرایب 268/0 و 595/0 ارائه شده است.
در ستون Approx. sig سطوح معنی داری این ارزش های همبستگی ارائه شده است. آزمون ها گودمن و کروسکال تاو و آزمون ضریب عدم قطعیت که به بررسی ارتباط میان متغیرهای اسمی می پردازند، در بخش انتهایی خروجی 17 ارائه شده اند.
در ستون Value، مقادیر ضریب همبستگی این آزمون ها و در آخرین ستون سمت راست، سطوح معنی داری مربوط به این همبستگی ها ارائه شده است.
خروجی مربوط به مابقی ضرایب همبستگی که در کادر ارتباطی شکل 11 قابل مشاهده اند، مشابه خروجی 17 قابل تفسیر و ردیابی هستند.
بنابراین نیازی به تشریح مثال ها و خروجی های مرتبط با آن ها نمی باشد.